Replicator mutator equation

Shared by Antoine Rideau thanks to Gael Raoul

On this page you will find how to simulate using Castor the replicator mutator equation

The replicator-mutator equation is a classical model from evolutionary biology that describes how a species reacts to selection by increasing a phenotypic trait \(x\). The selection is represented by a reproduction rate that increases linearly with \(x\) (the phenotype is actually the fitness of the individual), while the population is kept constant thanks to the continuous removal of individuals, uniformly among the traits present in the population. This is completed by a mutation term: the traits constantly mutate which is described by a diffusion term. This model is used to understand mutation-selection dynamics as a whole, even though it is more directly related to experimental setups used in experimental evolutionary biology, based on chemostats. This model has been used by R. Fisher to derive the so-called fundamental theorem of natural selection.

\[\partial_{t}u = \underbrace{\sigma \Delta_{x}u}_{mutations} + \underbrace{(x - \bar{x}(t))u}_{replication} \text{ , } t > 0,\]

where :

\(x \in \mathbb{R}\) : a one dimension fitness space,

\(u(t,x)\) : density of a population at time \(t\) and per unit of fitness,

\(\bar{x}(t):= \int_{\mathbb{R}}xu(x,t)dx\) : mean fitness at time \(t\) .

The population is considered constant, so

\[\int_{\mathbb{R}}u(x,t)dx = 1 .\]

Numeric simulation

N individuals are gathered within the population, each characterized by their fitness \(x_{i}\).

Ths population will evolve during gmax generations separated by dt .

// Parameters
int N = 1e3;        // Population
int gmax = 1e4;     // Number of generations
int Nplot = 1000;     // Number of generations plotted
double dt = 0.01;   // Time disretization
double sigma = 0.5; // Mutation

Initially, the population is distributed following a Gaussian distribution using randn .

// Initial data
auto parent = randn(1, N);

See label-randn .

Each generation :

1. Each individual has a probability \(\mathbb{P} = (x_{i})_{+} \times \Delta t\) ,where \((x_{i})_{+}\) stands for the positive part of \(x_{i}\) , to give birth to a child

// Probablity to give birth
auto birth = dt * maximum(parent, 0);

// Reproduction
auto reprod = rand(size(parent));

See maximum , rand , size .

who will inherit a fitness of \(x_{i} + X\) with \(X \sim \mathcal{N}(0, \sigma^2 \Delta t)\) .

// Children
auto children = parent + sigma * std::sqrt(dt) * randn(1, N);
children = eval(children(find(reprod < birth)));

// Update parent
parent = cat(2, parent, children);

See find , view , cat .

2. N individuals are uniformly choosen to survive.

// Kill parent to get N individuals
parent = eval(parent(randperm(numel(parent), N)));

See label-randperm , numel .

Code

#include <castor/matrix.hpp>
#include <castor/graphics.hpp>

using namespace castor;

int main(int argc, char const *argv[])
{
    // Parameters
    int N = 1e3;        // Population
    int gmax = 1e4;     // Number of generations
    int Nplot = 1000;     // Number of generations plotted
    double dt = 0.01;   // Time disretization
    double sigma = 0.5; // Mutation

    // Initial data
    auto parent = randn(1, N);

    // Initialize figure
    figure fig;

    // For each generation
    tic();
    for (int g = 1; g <= gmax; g++)
    {
        // Probablity to give birth
        auto birth = dt * maximum(parent, 0);

        // Reproduction
        auto reprod = rand(size(parent));

        // Children
        auto children = parent + sigma * std::sqrt(dt) * randn(1, N);
        children = eval(children(find(reprod < birth)));

        // Update parent
        parent = cat(2, parent, children);

        // Kill parent to get N individuals
        parent = eval(parent(randperm(numel(parent), N)));

        // Plot
        if (g % (gmax / Nplot) == 0)
        {
            plot(fig, parent, g * dt * ones(size(parent)), {"b"});
        }
    }
    toc();

    // Visu
    drawnow(fig);
    return 0;
}

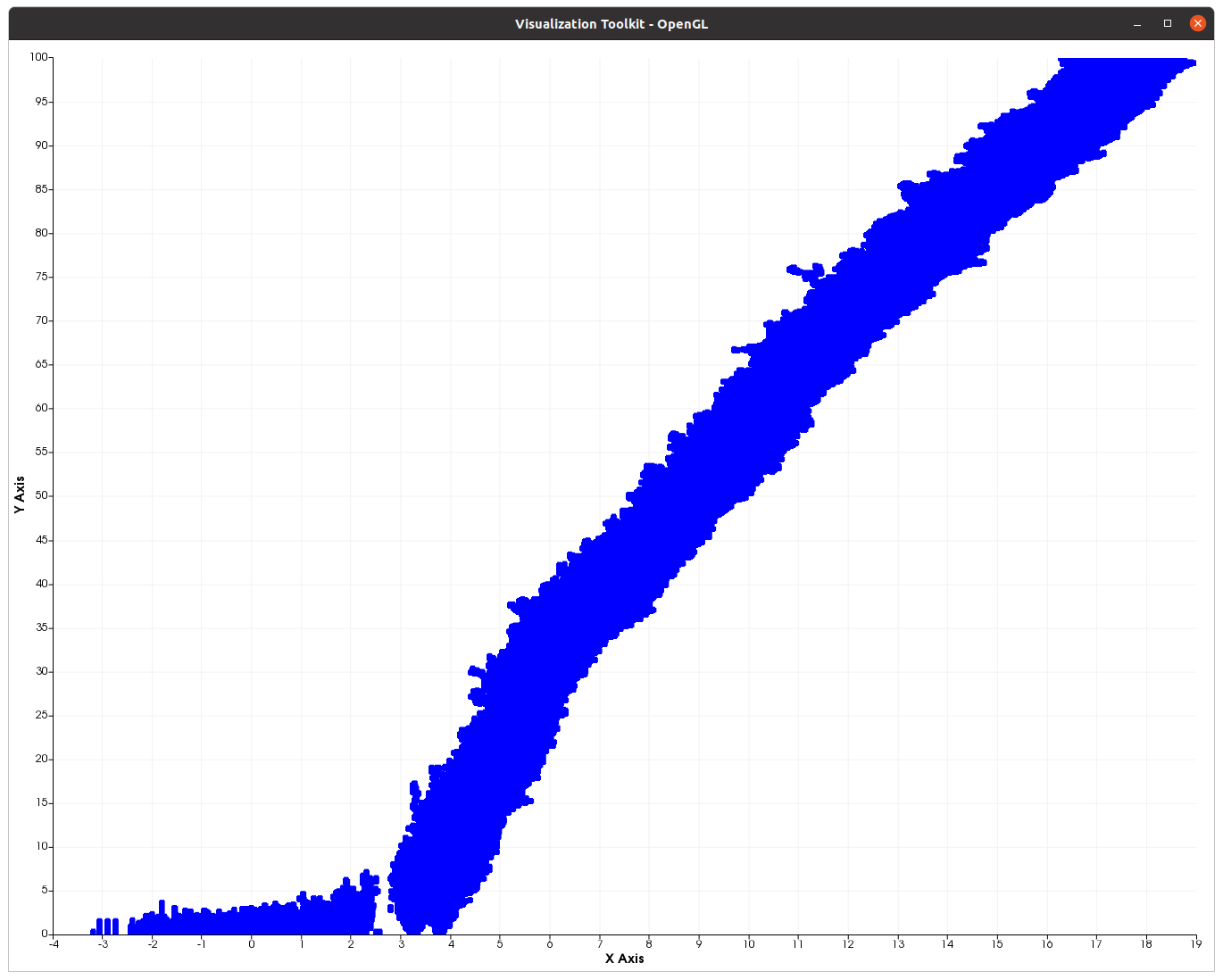
Fitness evolution of a 1 000 individuals’ population during 10 000 generations.

Reference

https://openlibrary.org/books/OL7084333M/The_genetical_theory_of_natural_selection.

https://www.cirm-math.fr/RepRenc/1315/PDFfiles1315.pdf